


刀疤五 发表于 2021-7-3 23:02
创新,创新,实在是创新!
感谢知识分享,楼主是个大公无私的人.


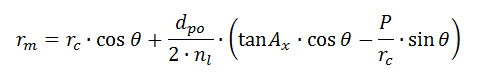
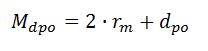
hyfjy 发表于 2021-7-4 21:44
吴工的解析法比较过硬,同时作图精准,故在推导过程中相得益彰,这样的技能是优秀的设计人所具备的,赞一个 ...
DD99 发表于 2021-7-5 16:13
一般不出手,出手不一般
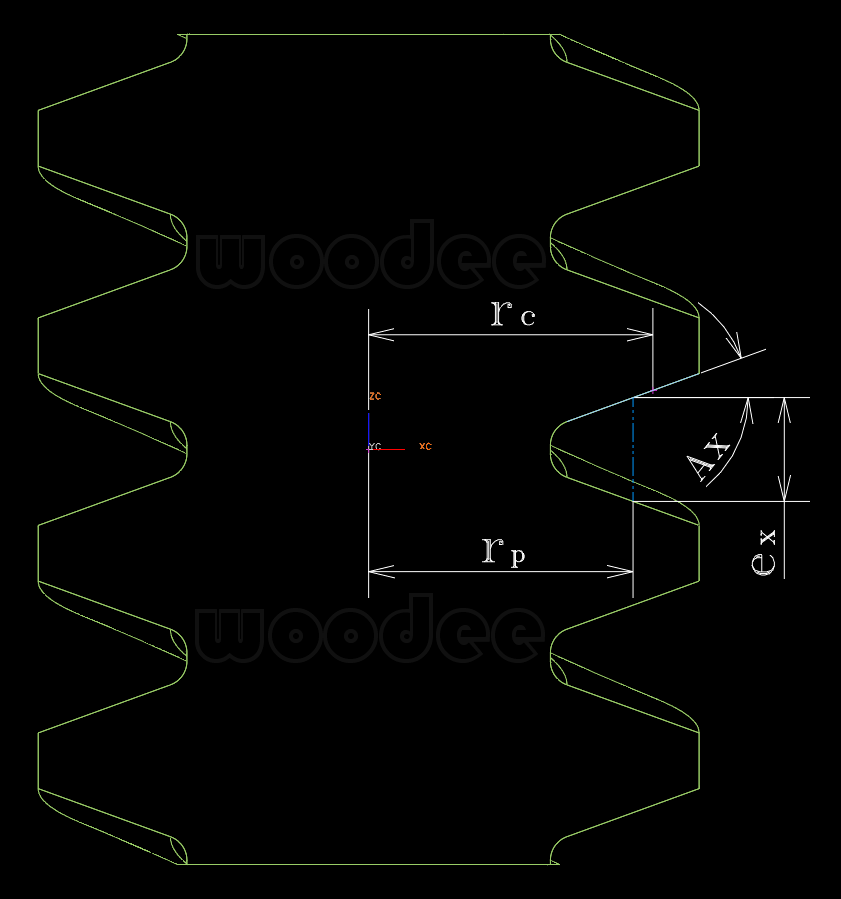
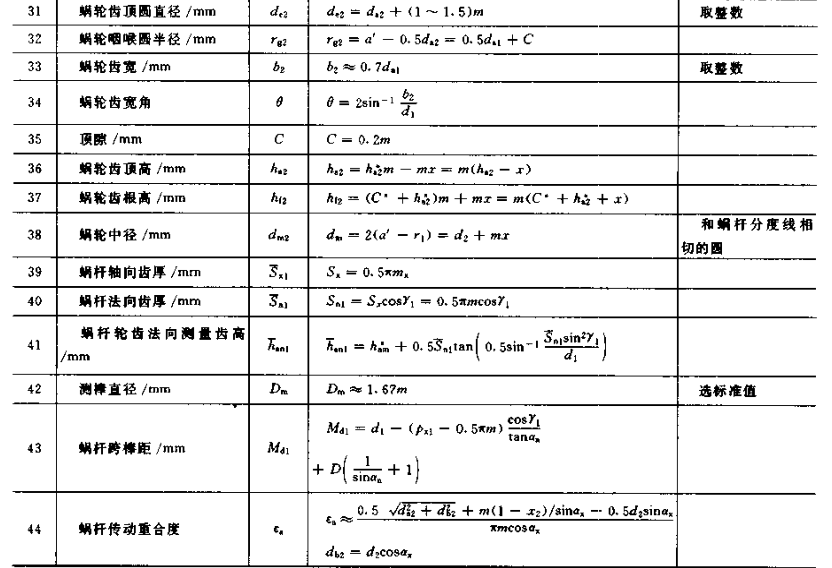
以前的有关蜗杆的资料上M值计算原来都是近似的计算。大神们的出手还是让 ...
yongxiangle1969 发表于 2021-7-5 20:48
厉害,向高手学习!顶一个!
DD99 发表于 2021-7-6 12:12
是这样的。ZI蜗杆的计算我是按齿轮方式计算的,M值与你们介绍的都一致的。对于ZA其它蜗杆因用的不多一般我 ...
番茄唐龙 发表于 2021-7-6 16:43
近半年来难的的好帖,顶
 |小黑屋|手机版|Archiver|齿轮论坛 www.gearbbs.com
|小黑屋|手机版|Archiver|齿轮论坛 www.gearbbs.com
GMT+8, 2025-6-26 21:32 , Processed in 0.366693 second(s), 19 queries , MemCache On.
Powered by Discuz! X3.4 Licensed
© 2001-2023 Discuz! Team.