求助按等滑动率计算变位系数?

yanta82

已知参数:   模数10   螺旋角10  齿数Z1=11  Z2=40  齿形角20度  顶隙系数0.25   中心距253  齿顶高系数为1.0
                ,按等滑动率的小齿轮变位系数是多少?(允许根切)  


              实际上我是想说齿轮节点外啮合的问题,这种传动要做磨损最小,理论是什么?是否还是按等滑动率(绝对值相等),案例不好找,上传一文章,抛砖引玉.

48824305

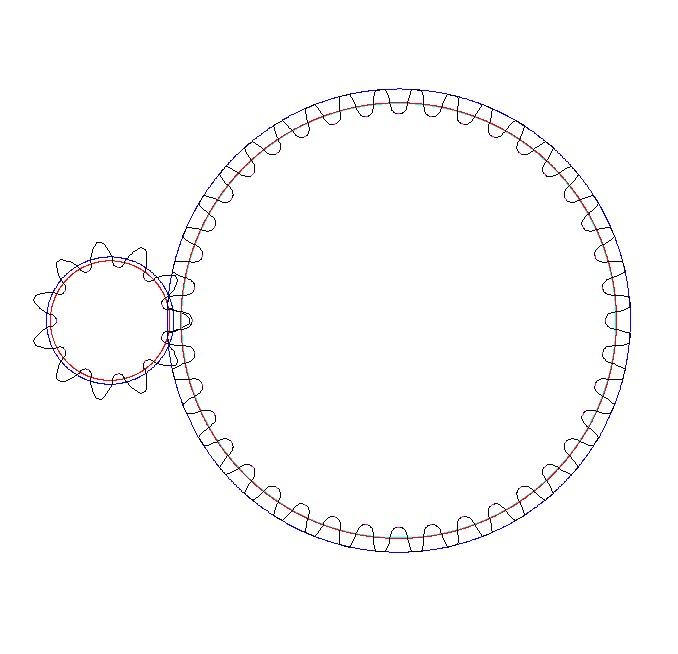
输入参数:
法面模数Mn=10.0
端面模数Mt=10.1543
齿数z1=11
齿数z2=40
法面分度圆压力角αn=20.0°
端面分度圆压力角αt=20.2836°
齿顶高系数han=1.0
顶隙系数cn=0.25
螺旋角β=10.0°
齿根曲线圆角系数kc=0.38
齿轮z1齿宽B1=222.101
齿轮z2齿宽B2=217.101
齿轮第二公差组精度等级IT=7

计算结果:
实际中心距a'=253.0
中心距极限偏差: ±40.5 μm
最小法向侧隙Jbnmin= 324 μm(参考值)
(由Jbnmin=2/3*(0.06+0.0005*ai+0.03*mn)计算而来)
最小侧隙Jnmin= 210 μm(参考值)
(按GB10095-88参考值)
标准中心距a=258.934
中心距变动因素У=-0.584364
啮合角α'=16.2627°
齿高变位因数ΔУ=0.0535143
法面总变位因素Σχn=-0.539039
外啮合齿轮副z1,z2 齿数比u12=3.63636
齿轮z1的法面变位因数χn1=0.4
齿轮z2的法面变位因数χn2=-0.939039
端面总变位因数Σχt=-0.53085
齿轮z1的端面变位因数χt1=0.393923
齿轮z2的端面变位因数χt2=-0.924773
齿轮z1齿顶圆直径da=138.61    齿轮z1齿根圆直径df=94.6969
齿轮z1分度圆直径d=111.697    齿轮z1基圆直径db=104.77
齿轮z1的固定弦齿厚sf1=16.4416
齿轮z1的固定弦齿高hf1=10.4645
齿轮z1的当量齿分度圆弦齿厚sv1=18.5387
齿轮z1的当量齿分度圆弦齿高hv1=14.2075
齿轮z1的公法线跨测齿数k1=2
齿轮z1的公法线长度w1=48.6276
齿轮z1的法面齿顶厚sa1=4.39599
对于硬齿面,必须sa1>0.25*mn=2.5
对于软齿面,必须sa1>0.40*mn=4.0
齿轮z2齿顶圆直径da=406.303    齿轮z2齿根圆直径df=362.39
齿轮z2分度圆直径d=406.171    齿轮z2基圆直径db=380.983
齿轮z2的固定弦齿厚sf2=7.83446
齿轮z2的固定弦齿高hf2=-1.35954
齿轮z2的当量齿分度圆弦齿厚sv2=8.86355
齿轮z2的当量齿分度圆弦齿高hv2=0.687267
齿轮z2的公法线跨测齿数k2=3
齿轮z2的公法线长度w2=73.2324
齿轮z2的法面齿顶厚sa2=8.82685
对于硬齿面,必须sa2>0.25*mn=2.5
对于软齿面,必须sa2>0.40*mn=4.0

端面重合度εα=1.50787 (应大于或等于1.0,一般≥1.2)

      z1的滑动率η12_1=74.546
      z2的滑动率η12_2=5.47718(滑动率η12_1,η12_2应该接近,相等最为理想)

      z1的压强比ζ1=6.84185
      z2的压强比ζ2=0.857103(压强比ζ应该小于1.4~1.7)

压强比是用来表示齿廓各点接触应力与在节点处接触应力的比值,其分布情况与滑动率分布情况相似;滑动率η是用来表示齿廓磨损的,一般要求η<4.0

      轴向重合度εβ=1.2 (应大于或等于1.0,一般≥1.2)

  齿宽系数(b/d)  ψd=  1.94366
-----------------------------------------
已知中心距a'=253.00000000,按齿轮z1,z2滑动率(齿廓磨损率)相等计算变位系数无解

已知中心距a'=253.00000000,按齿轮z1,z2压强比相等(ζ1=ζ2)计算变位系数无解


齿轮z1法向齿顶厚为0.25*mn时的变位系数为: 0.637058
(对于硬齿面,必须小于此变位系数.)
此时齿轮z2的变位系数为: -1.1761
齿轮z1法向齿顶厚为0.4*mn时的变位系数为: 0.452789
(对于软齿面,必须小于此变位系数.)
此时齿轮z2的变位系数为: -0.991828

z1不根切的最小变位系数为: 0.326385  (所选变位系数必须大于此根切的变位系数.)
z2不根切的最小变位系数为: -1.44951  (所选变位系数必须大于此根切的变位系数.)

滑动率越大,齿廓磨损率越大,噪音越大,寿命越短.按齿轮滑动率(齿廓磨损率)相等计算变位系数可有效地减小小齿轮的滑动率,减小齿廓磨损,降低噪音,延长小齿轮的寿命.
  小齿轮变位系数越小,齿轮副的端面重合度εα越大.

yanta82

回复 48824305 的帖子

参数瞎编的,是为了探讨问题用的,不管它了,只看1.0的
讨论一下:(只考虑磨损)滑动率是有方向性的,以正负号表示,当绝对值相等时,可认为是磨损最轻的,此时的变位系数是最优的?

48824305

绝对值相等时,符号为正,可认为是磨损最轻的

yanta82

回复 48824305 的帖子

没明白,既然绝对值相等,就无所谓正负号了,

yanta82

这样说吧,两组的滑动率分别处是(小齿轮1.5, 大齿轮1.5),另一组是(小齿轮1.5,大齿轮是-1.5),抗磨损一样吗?假设它们其它参数都一样.

陈飞

正负号表示滑动的方向。

yanta82

从概念上讲,(其它条件认为已确定)磨损量大小是由齿面滑动速度(大小齿轮相对速度)体现的, 滑动率越小, 磨损量越有利,当大小齿轮滑动率接近时,此时滑动率最小,即认为磨损量最小,这是大多手册上说的,公式也都一样,另外滑动率正负号只是齿面滑动方向不同而已。
以上是我的判断，不对的，请指正
在上例中我也是无解,然后将程序改了下,以为可以解出来,如下   
χ1=0.1376 η1=-4.069   η2=4.06     当时以为这是滑动率最小了，其实又测试一下还有
χ1=-0.27  η1=-2.408   η2=2.408     滑动率更小，再随机输入两组
χ1=-0.539 η1=-2.139 η2=1。65
χ1=-1.2 η1=-1.79 η2=-0.41          可看到滑动率的最小值无法找到，
通过上边1楼的例子可看到，通过判断两齿轮齿根处的滑动率相等来找变位系数有时做不到，但确实在齿轮各方面都允许的情况下，有一合适的变位系数对应最小的滑动率（可能不相等，也可能有一正一负，但可不管它，只要是最小就行），如果我的看法没错，就可以在一定条件限制下（此条件可更改。比如小齿轮的变位系数范围在正负1.0变化）,找到这个值,这样,扩大了通过两齿轮齿根处的滑动率相等来找变位系数的应用范围.
这是我发帖的目地,48824305网友给了我一些启发.

yanta82

"肯定是不一样的，外啮合的齿轮副应都为正值内啮合的齿轮副，外齿轮就应为正，有的资料上说因内齿轮是静止的，故内齿轮的齿面相对于外齿轮的齿面滑移率就是相啮合外齿轮的的值。  发表于 1 小时前 "

滑移率节点处为0,节点处两个方向的滑移率相反(一正一负),已是定论.
既然"内齿轮是静止的",那它就是行星传动,行星传动没有静止这一说,所谓静止是相对的,因此,"故内齿轮的齿面相对于外齿轮的齿面滑移率就是相啮合外齿轮的的值。"是不对的.

yanta82

"这样的话,通过两齿轮滑动率相等找变位系数,就变成了由滑动率最小找变位系数.  发表于 半小时前 "
是这样的,我已将程序改了,只不过是由滑动率 绝对值 最小找变位系数,已测试过,与"通过两齿轮滑动率相等找变位系数"的结果是一致的,我设想如果某一齿轮的啮入点与啮出点在节点的同一側的话,还想找最小滑动率,上式就能实现,但实际这种例子很罕见,也不是没有,既然想到这了,就改了程序(预防万一),也不会对用齿轮滑动率相等找变位系数有影响.就像行星传动为了得到精密的传动比,而不满足装配条件"(Zb+Za)/np等于整数"一样,都有特例.