- UID
- 15458
- 好友
注册时间2008-10-6
威望值 点
最后登录1970-1-1
激情值 点
积分2978
认证分 分
齿轮币 枚
回帖0
|
本帖子中包含更多资源。
您需要 登录 才可以下载或查看,没有账号?注册
x
本帖最后由 刀疤五 于 2017-4-20 13:44 编辑
问题:N个顺序点坐标X(I),Y(I)构成的样条曲线,求X为某值时,Y=?
方法是构造三次样条进行插值, 书本上讲了三种构造方法.
1.自然样条(通用做法.把首尾点的二阶导数强行定为0).
2.固支样条(已知首尾点导数或者说已知首尾点的方向切矢).
3.周期样条
近来发现MATLAB还有一种非扭结样条,而且把非扭结样条当成默认的插值计算方法.
采用 函数 Y=SIN(X) X范围0度到270度,点数N=55,X变步长,即按:
X1=0
X2=2.5
X3=10...
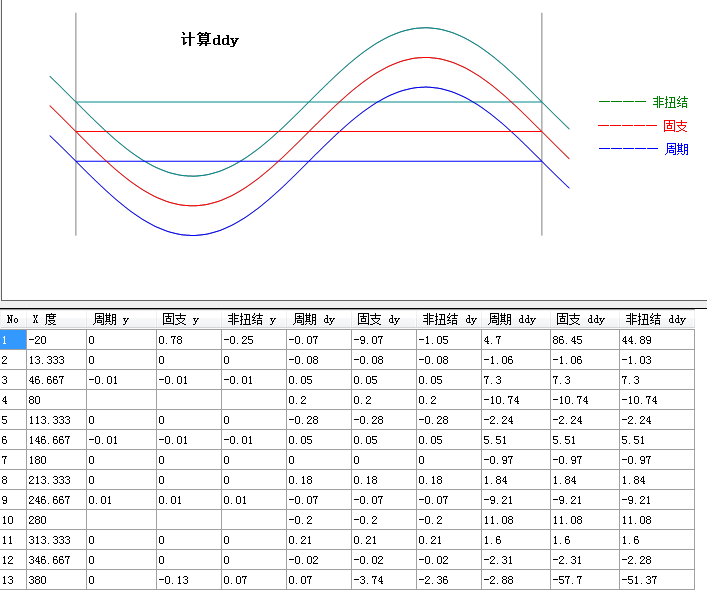
用这55个点分别用自然样条,固支样条,非扭结样条进行插值计算.X的取值范围从-20到290度,可以发现固支样条最准,非扭结样条也很可靠,自然样条不可靠.(图片中灰色线是用函数来计算出的值)
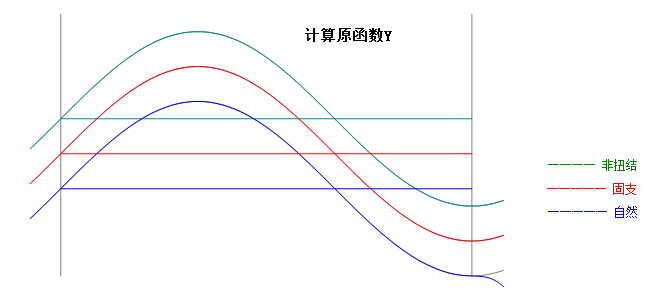
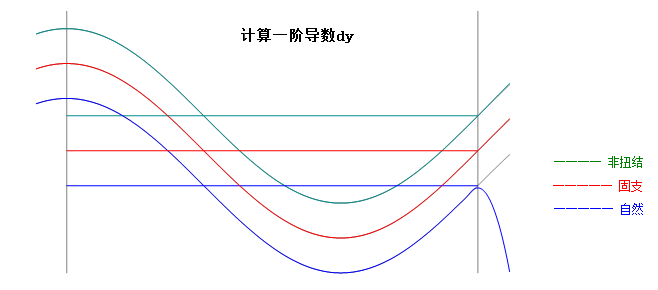
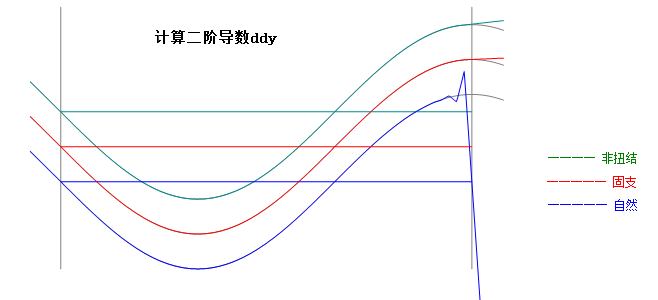
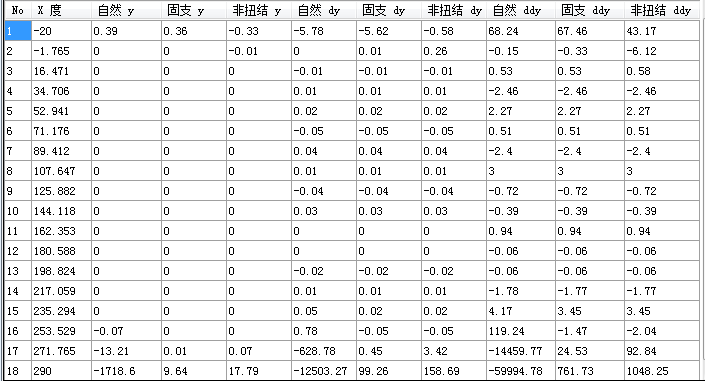
固支样条的前提是必须知道首尾点的一阶导数,在实际中,已知条件只是一系列点.根本不知道首尾点导数.因此,按MATLAB做法选非扭结样条.从图形中可以发现,三种方法,在区间(0,270)度内,且不靠近端点的区域,插值计算均是可靠的.具体计算结果与原函数的误差如下(放大了10000倍).
如果曲线封闭,采用周期样条,是最准的. 函数 Y=SIN(X) X范围0度到360度,点数N=73,X变步长.结果如下:
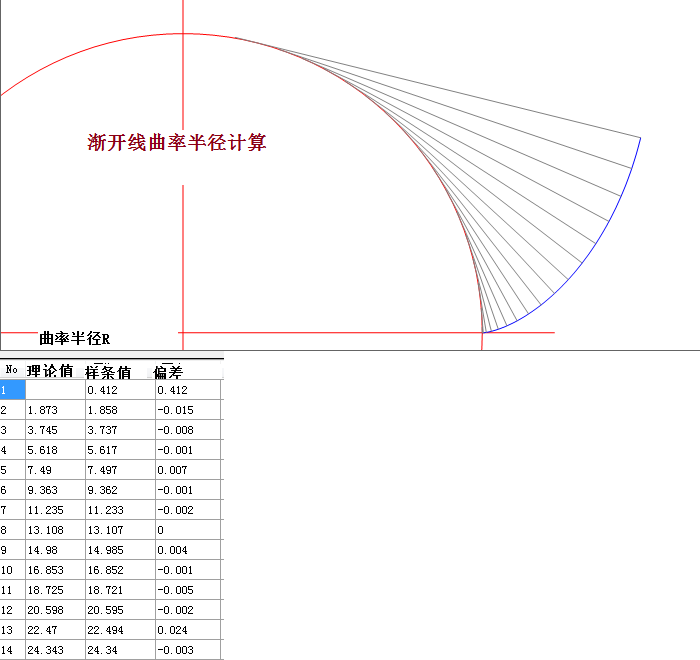
剃增步长,渐开线曲率半径的计算
|
|
 |小黑屋|手机版|Archiver|齿轮论坛 www.gearbbs.com
|小黑屋|手机版|Archiver|齿轮论坛 www.gearbbs.com